Multi-Asset Equity and Variance Linked Notes
In response to the increased popularity of multi-asset equity and variance linked notes, e.g. auto-callables, reverse convertibles, basket variance structures and callable equity and/or interest rate range accruals, SciComp is pleased to announce support for these structures using both PDE (partial differential equation) and Monte Carlo based pricing methods.
Source Code and Interfaces
Pricing model source code for these and related contracts can be generated by SciFinance®, SciComp’s in-house model development technology. SciFinance® automatically generates efficient C++ or CUDA derivatives pricing model source code from specifications written in an intuitive, finance-specific language. A wide range of interfaces are available with SciFinance® including .NET, COM, Java, Excel, and Python.
Multi-asset equity and variance linked note pricing models are also available as stand-alone Excel spreadsheet and add-ins or Windows/Unix executables that are readily customizable.
Features and Underlyings
Possible underylings include (but are not limited to) single assets, indices, and average or best/worst performance baskets. For up to three assets under local volatility dynamics a PDE method using SciComp’s predictor-corrector ADI solvers is generally faster, while the Monte Carlo method is applicable for larger baskets, complex path dependencies or more complex dynamics.
Among features easily describable are simple or moving knock-in and knock-out (auto-call) barriers which may be either discretely or continuously monitored; discrete, absolute or proportional dividends; quanto features, simple, range accrual, and/or snowball coupons; realized variance; and Asianing in and out of average quantities. Many of these may be invoked in Monte Carlo models in a single line using a provided macro library.
PDE Models
In PDE models finite difference grids may be structured to place barriers on grid points (continuously monitored) or at midpoints (discretely monitored), and densely spaced around barriers for rapid convergence and smooth Greeks even with highly discontinuous payoffs.
Monte Carlo Models
In Monte Carlo models Brownian bridge continuity corrections may be specified for continuous monitoring of barriers while high dimensional quasi-random sequences greatly reduce variance. In either method sensitivities to any underlying model and contract parameters can be easily defined.
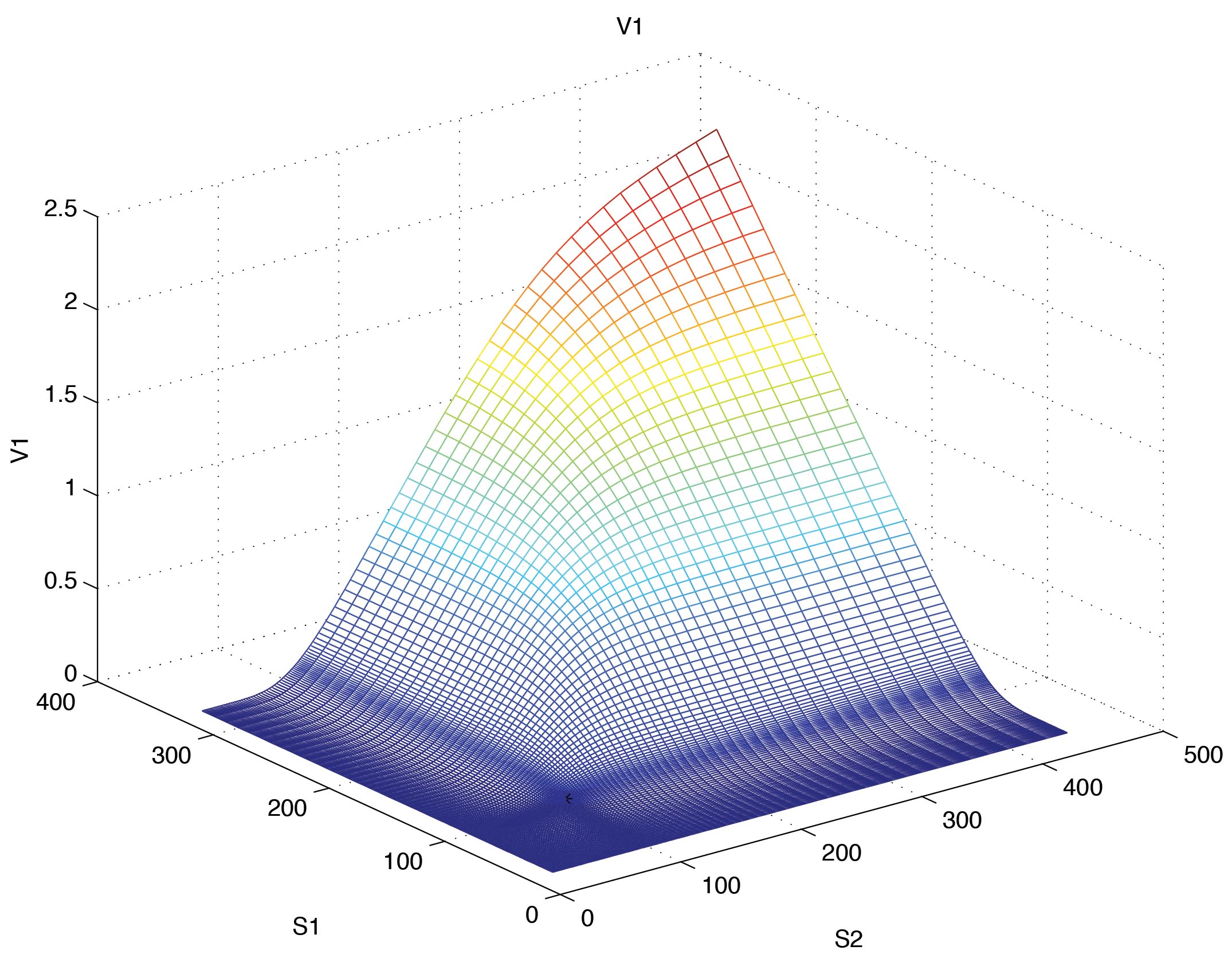
Present value of the worst-of call maturity payment of a two-asset equity linked note.

